GEOMETRÍA PLANA
Un carpintero utiliza un cepillo para “aplanar” una tabla. El departamento del Petén es un departamento plano en su mayor parte. La palabra PLANO tiene un nuevo significado para usted ahora que comienza a estudiar Geometría.
Cada cosa en la vida tiene ciertas palabras que se relacionan entre si para darle significado.
En Geometría hay ciertas palabras que debemos aprender con el fin de comprender esta fascinante materia.
La Geometría es utilizada todos los día en nuestra vida, usted no podría dormir en una cama redonda, duerme en una cama rectangular.
Usted tiene un escritorio donde labora , rectangular también.
Incluso las herramientas de la agricultura como el azadón o la piocha han sido construidas basados en la geometría. Por ejemplo: la piocha; tiene un pico en forma de triangulo con el que Ud. puede cavar hoyos.
ANGULOS

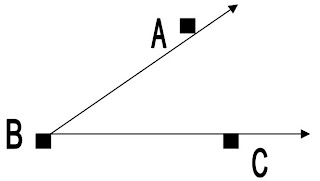 Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>
Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>
Otra forma de rotular ángulos es usando la letra del vértice solamente, < B por ejemplo: pero si la figura tiene más ángulos con vértices B entonces no puede usar esta forma.
Una tercera forma de nombrar ángulos es utilizar letras minúsculas dentro de la figura como las del ejemplo siguiente.


m = medida.
< = ángulo
ABC = nombre del ángulo
39 = lo que mide el ángulo.
° = Este circulito pequeñito significa grados.

 Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.
Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.
En el ejemplo anterior podemos ver que sumando las medidas de ambos 40 + 50 = 90.
Dicho en términos geométricos: m angulo ABD + m angulo DBC = 40° + 50° = 90°
A partir de ahora utilizaremos más las abreviaturas, trate de memorizar que quiere decir cada símbolo y tenga en mente que las letras señalan los puntos del ángulo.
Un carpintero utiliza un cepillo para “aplanar” una tabla. El departamento del Petén es un departamento plano en su mayor parte. La palabra PLANO tiene un nuevo significado para usted ahora que comienza a estudiar Geometría.
Cada cosa en la vida tiene ciertas palabras que se relacionan entre si para darle significado.
En Geometría hay ciertas palabras que debemos aprender con el fin de comprender esta fascinante materia.
La Geometría es utilizada todos los día en nuestra vida, usted no podría dormir en una cama redonda, duerme en una cama rectangular.
Usted tiene un escritorio donde labora , rectangular también.
Incluso las herramientas de la agricultura como el azadón o la piocha han sido construidas basados en la geometría. Por ejemplo: la piocha; tiene un pico en forma de triangulo con el que Ud. puede cavar hoyos.
DEFINICIONES
PUNTO: Un punto imaginario o escrito como el que finaliza esta frase.
Pero en Geometría el punto es la parte más pequeña que usted se puede imaginar de un punto.
PUNTO: Un punto imaginario o escrito como el que finaliza esta frase.
Pero en Geometría el punto es la parte más pequeña que usted se puede imaginar de un punto.
LINEA: Una serie de puntos conectados unos con otros de manera recta. La línea en geometría está hecha de puntos.
SEGMENTO DE LÍNEA: En cualquier línea el segmento es una parte con principio y fin.
RECTA: En una línea, una parte que consiste de un punto inicial y todos los puntos de esa línea desde ese lugar donde está el punto. Una RECTA no tiene punto final. Imagine una recta como una luz de una linterna apuntada hacia el cielo. El punto inicial es la linterna y la luz viaja hacia el infinito.
POLÍGONO: Una figura cerrada hecha de tres o más segmentos de línea.
POLÍGONO: Una figura cerrada hecha de tres o más segmentos de línea.
ANGULOS
Si dos rayas inician desde el mismo punto hacia distintos lados usted obtiene un ángulo. El punto donde comienzan las dos rayas se llama VÉRTICE DEL ANGULO. Las dos rayas se llaman lados del ángulo.

ROTULANDO ÁNGULOS
Los ángulos pueden ser rotulados o nombrados utilizando letras.
 Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>
Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>Otra forma de rotular ángulos es usando la letra del vértice solamente, < B por ejemplo: pero si la figura tiene más ángulos con vértices B entonces no puede usar esta forma.
Una tercera forma de nombrar ángulos es utilizar letras minúsculas dentro de la figura como las del ejemplo siguiente.

MEDICIÓN DE ÁNGULOS
Piense en cada lado de un ángulo como si fueran las manecillas de un reloj despertador, de esos de cuerda. Imagine que usted necesita darle cuerda al reloj porque se le terminó y que hay que ponerle la hora exacta. Los números o signos que hay alrededor del reloj le ayudarán a mover las manecillas tanto como lo necesite.
La unidad para medir un ángulo es el grado y el instrumento para medir ángulos es el transportador.
El transportador es una regla curva que está dividida en 180 partes iguales. La de arriba es una gráfica que ilustra como debemos utilizar el transportador para medir un ángulo.
El ángulo ABC que está siendo medido en esta gráfica mide 39°.
La unidad para medir un ángulo es el grado y el instrumento para medir ángulos es el transportador.
El transportador es una regla curva que está dividida en 180 partes iguales. La de arriba es una gráfica que ilustra como debemos utilizar el transportador para medir un ángulo.
El ángulo ABC que está siendo medido en esta gráfica mide 39°.

Como dije al principio, en Geometría debe acostumbrarse a términos y signos propios de la Geometría. No se preocupe si no se los memoriza todos rápidamente, solo trate de conservar este libro, no prestarlo, no fotocopiarlo, de esa forma le durará bastante y cada vez que necesite recordar algo podrá venir hasta aquí y consultarme.
Volvamos a la imagen ahora.
El vértice del ángulo se coloca exactamente en el medio del transportador, el lado del ángulo marcado con la letra A ha sido colocado exactamente en la posición 0° (Cero grados) y el lado marcado C nos muestra la medida del ángulo. 39°. Para abreviar medida en geometría usamos la letra minúscula m.
Toda esa palabrería que nos ha ocupado esta columna se puede abreviar simplemente así.
así. m angulo ABC = 39°. Volvamos a la imagen ahora.
El vértice del ángulo se coloca exactamente en el medio del transportador, el lado del ángulo marcado con la letra A ha sido colocado exactamente en la posición 0° (Cero grados) y el lado marcado C nos muestra la medida del ángulo. 39°. Para abreviar medida en geometría usamos la letra minúscula m.
Toda esa palabrería que nos ha ocupado esta columna se puede abreviar simplemente así.
m = medida.
< = ángulo
ABC = nombre del ángulo
39 = lo que mide el ángulo.
° = Este circulito pequeñito significa grados.
ANGULO RECTO
Es un ángulo especial cuyos lados forman una esquina cuadrada. Un ángulo recto mide exactamente 90°
 En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo.
En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo.
 En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo.
En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo. ANGULO LLANO
Este es un tipo especial de ángulo. Sus lados apuntan exactamente en sentidos opuestos formando una linea recta. Si usted mide un ángulo llano con un transportador encontrará que miden exactamente 180°. Esta es la medida más grande que cualquier ángulo puede tener.

TÉRMINOS GEOMÉTRICOS
GRADO: La unidad utilizada para medir ángulos.
TRANSPORTADOR: El instrumento utilizado para encontrar los grados de un ángulo.
ANGULO RECTO: Un ángulo cuya medida da exactamente 90 grados. Un ángulo recto forma una esquina cuadrada
ANGULO LLANO: Un ángulo cuya medida es exactamente 180°. Un ángulo llano forma una linea recta.
PARES ESPECIALES DE ÁNGULOS
Algunos ángulos son comúnmente encontradnos en pares. Los tres pares mas importantes son explicados de aquí en adelante.
Ángulos complementarios: Si dos ángulos juntos totalizan 90° se les llama ángulos complementarios.
 Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.
Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.En el ejemplo anterior podemos ver que sumando las medidas de ambos 40 + 50 = 90.
Dicho en términos geométricos: m angulo ABD + m angulo DBC = 40° + 50° = 90°
A partir de ahora utilizaremos más las abreviaturas, trate de memorizar que quiere decir cada símbolo y tenga en mente que las letras señalan los puntos del ángulo.

ANGULOS VERTICALES
Es otro par importante de ángulos. Son ángulos opuestos formados donde dos líneas rectas cruzan. Los ángulos verticales siempre tienen la misma medida.

Estudie este diagrama, vea que los dos ángulos angulo c y angulo d son ángulos verticales porque están de lados opuestos.
También angulo a>
ANGULOS FORMADOS POR LINEAS PARALELAS Y TRANSVERSALES
Líneas paralelas son como las líneas que un estudiante hace con su regla en un cuaderno para dibujar una línea de ferrocarril que cruza una planicie. Líneas paralelas se mantienen siempre a la misma distancia una de la otra y nunca se unen. He aquí un ejemplo:
Líneas paralelas son como las líneas que un estudiante hace con su regla en un cuaderno para dibujar una línea de ferrocarril que cruza una planicie. Líneas paralelas se mantienen siempre a la misma distancia una de la otra y nunca se unen. He aquí un ejemplo:

Por el otro lado, una línea transversal es una que cruza por sobre dos o más líneas paralelas como el siguiente ejemplo: Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.
Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.
 Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.
Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.TÉRMINOS:
Líneas Paralelas: Líneas que van una al lado de otra, siempre a la misma distancia pero que nunca se juntan. Como las líneas del ferrocarril.
Línea Transversal: Una línea que corta o cruza dos o más líneas paralelas. Algunos matemáticos las llaman secantes.
Líneas Paralelas: Líneas que van una al lado de otra, siempre a la misma distancia pero que nunca se juntan. Como las líneas del ferrocarril.
Línea Transversal: Una línea que corta o cruza dos o más líneas paralelas. Algunos matemáticos las llaman secantes.
Ejemplo:
En los siguientes ejemplos, usted verá tres pares especiales de ángulos que se forman cuando las líneas paralelas son cruzadas o cortadas por una transversal. La primer clase se llama ángulos correspondientes. El diagrama de la siguiente página muestra que
En los siguientes ejemplos, usted verá tres pares especiales de ángulos que se forman cuando las líneas paralelas son cruzadas o cortadas por una transversal. La primer clase se llama ángulos correspondientes. El diagrama de la siguiente página muestra que


asco
ResponderEliminarMUY BIEN
ResponderEliminarEXELENTE
Muy poca información sobre lineas transversales ����������������
ResponderEliminar