 |
Geometría
La geometría fue, primero, la ciencia de la medida de las extensiones (geo = tierra; metrón = medida). Lo que se aprendió a medir (con los geómetras griegos) fue la extensión de una línea, recta o curva; de una superficie limitada por líneas y de un volumen limitado por superficies. Pero rápidamente la expresión medir adquirió entre los griegos un sentido muy general de "establecer relaciones". Estas relaciones eran de dos clases:
Relaciones de posición que se enuncian por proposiciones tales como " La recta D es paralela a la recta D’", " la recta D es tangente al círculo C", etc.
Relaciones métricas, tales como "el segmento AB es triple del segmento AC", "la relación entre la longitud de la circunferencia y su diámetro es un número que ninguna fracción puede definir", etc.
Para establecer estas relaciones tan numerosas y variadas, los geómetras de la antigüedad pusieron a punto un método que se convertiría más adelante en el método matemático por excelencia: la demostración.
Todo el arte de los geómetras griegos consistió en reunir un conjunto importante de teoremas enlazados mediante largas cadenas de razones - como dijo Descartes- a algunos principios primeros. Este "corpus" es la geometría euclidiana.
Precisamente, el valor estético de la construcción euclídea y la trascendencia intelectual de su programa consiste en haberse propuesto eslabonar el conjunto de axiomas, definiciones y razonamientos con arte y perfección. En vez del confuso montón de intuiciones y demostraciones de los geómetras anteriores, Euclides seleccionaba unos pocos conceptos fundamentales y unas pocas relaciones entre estos conceptos, enunciadas explícitamente, para, desde aquí, pasar a la creación de nuevos conceptos y al descubrimiento de nuevas relaciones entre ellos.
La geometría de Euclides, la geometría de Descartes, la geometría de Riemann o la de Lovachevski, etc., son unas teorías deductivas. Los entes de los cuales tratan se llaman figuras y podemos dar de ellas diversas imágenes que nos permiten comunicar con nuestros semejantes. Estas imágenes pueden ser símbolos figurativos, ecuaciones, etc.
La Geometría no euclídea: Geometría para la que no es válido el axioma de paralelismo de Euclides (quinto postulados de Euclides).
La Geometría hiperbólica: Geometría no euclídea en la cual el postulado de las paralelas se sustituye por otro según el cual desde un punto exterior a una recta se pueden trazar al menos dos paralelas a ella, las cuales separan a todas las rectas que pasan por el punto en dos clases. Una, la de las que cortan a la recta dada y otra, la de las que no tienen puntos comunes con esa recta.
La Geometría elíptica: Geometría no euclídea en la cual el quinto se sustituye por otro el cual desde un punto exterior a una recta no se puede trazar ninguna recta paralela a ella.
La Geometría proyectiva: Geometría cuyos objetos son los espacios proyectivos y sus aplicaciones propias, las proyectividades.
Reseña histórica.
Es importante, antes de emprender un estudio de la geometría Euclidiana, revisar algunos antecedentes históricos que nos permita tener una visión general de su desarrollo. Tanto Proclos, como Herodoto, consignan en sus escritos que la geometría tuvo sus orígenes en Egipto con la medición de áreas, ya que el río Nílo, al desbordarse, borraba las señales que limitaban los terrenos de los agricultores. Según reseña el historiador Herodoto, en tiempos de Ramses II (1300 A. C.) la tierra del valle del Nilo se distribuía en terrenos rectangulares iguales por los cuales se debía pagar un impuesto anual, pero cuando el río invadía los terrenos, el agricultor tenía que avisar al rey lo sucedido, enviando éste a su vez a un supervisor que medía la parte en que se había reducido el terreno para que pagara sobre lo que quedaba, en proporción a impuesto que se había fijado. Precisamente, la palabra Geometría significa «medición de tierra». Afirma Herodíto que habiéndose originado la geometría en Egipto, país después a Grecia. Hay evidencias históricas, también, de aplicaciones, geométricas, algunos miles de años antes de nuestra era en regiones tales como Mesopotamia, (comprendida entre los ríos Tígris y Eufrates) y algunas regiones del centro, sur y este de Asia, en las cuales se desarrollaron grandes obras de ingeniería en la construcción de edificios y sistemas de canalización y drenaje. Los babilonios (Mesopotamia), habían desarrollado la aritmética a muy buen nivel, permitiéndoles hacer cálculos astronómicos y mercantiles. Conocían reglas (2000 - 1600 A. C.) para calcular el área de triángulos, rectángulos, trapezoides, volumen de paralelepípedos rectangulares, volumen de prisma recto, volumen de cilindro circular recto, del área del círculo (con aproximación 71= 3). Hay vestigios de que en esa época era también conocido el teorema de Pitágoras. La geometría babilónica y egipcia, como podemos apreciar era eminentemente práctica. Se le utilizaba para resolver una serie de problemas de la vida cotidiana y no como una disciplina especial, metódica. A La matemática prehelénica se, le veía como una colección de reglas para hacer cálculos que les permitía obtener resultados satisfactorios para las necesidades de la época. Alcanzaron un gran desarrollo de, la habilidad operatoria, pero sin que se presentara un sólo caso de razonamiento deductivo, como se presentó posteriormente en la etapa griega. Las relaciones matemáticas de los babilonios y egipcios fueron esencialmente formuladas, mediante el método de experimentación y error, de manera empírica, de ahí que muchas de ellas eran definitivamente erróneas.
Cualquiera que sea la conexión entre las matemáticas griegas y las de oriente, los griegos trasformaron la geometría en algo muy diferente del conjunto de conclusiones empíricas que usaron sus predecesores. Los griegos, propusieron que los hechos matemáticos deben ser establecidos por razonamientos deductivos. Las conclusiones matemáticas deben ser confirmadas mediante una demostración lógica, no por experimentación. No se sabe con certeza por qué los griegos decidieron alrededor de 600 A. C. abandonar el método empírico de obtener conocimientos matemáticos y adoptar el de razonamiento deductivo. Tal vez una de las causas sea su estructura social, pues los filósofos, artistas y matemáticos pertenecían a una clase social privilegiada que desdeñaban los trabajos manuales y las ocupaciones prácticas que eran desempeñadas por las clase más bajas, lo cual permitía a las clases privilegiadas dedicar tiempo a pensar, pues por aquel tiempo los griegos eran muy dados a hacer grandes teorías para explicar el mundo. De hecho no existen fuentes para el estudio de la geometría griega antigua, la única fuente de que se dispone, de tal época, es la obra de Proclo, conocida con el nombre de sumario de Eudemo, escrita en el siglo V D. C., y en la cual se esboza de manera muy breve el desarrollo de la geometría, desde la antigüedad hasta Euclides. El sumario de Eudemo debe su nombre a que está basado en una serie de trabajos escritos por Eudemo, discípulo de Aristóteles. Según lo relaciona el sumario de Eudemo, la geometría demostrativa se inicia en 600 a. c. con Tales de Mileto, comerciante originario de Mileto, en la costa de Asia Menor. Conocido como uno de los «siete hombres sabios» de la antigüedad, también se dedico a la filosofía, matemática, astronomía y política, frecuentemente se le llama «el padre de la geometría demostrativa», pues aplicó a sus trabajos los procedimientos del razonamiento deductivo. A Tales se le acreditan los siguientes resultados, geométricos:
Un diámetro biseca un círculo.
Los ángulos a la base de un triángulo isósceles son iguales.
Los ángulos opuestos formados por dos rectas que se intersecan son iguales.
Dos triángulos son congruentes si tienen un lado y dos ángulos iguales.
El ángulo inscrito en un semicírculo es ángulo recto (los babilonios conocían esto 1400 a los antes).
El siguiente matemático griego famoso en el sumario de Eudemo es Pitágoras, nacido aproximadamente en el año 572 a. c. en la isla de Samos, isla del mar Egeo, cercano a la ciudad de Mileto. Pitágoras, 50 años más joven que tales, razón por la cual se cree que fue discípulo de éste, es famoso no solo por el teorema que lleva su nombre, sino por sus estudios de música y sobre todo por haber fundado en el puerto de Crotona, al sur de Italia, la famosa escuela Pitagórica para el estudio de la filosofía, la música, la matemática y las ciencias naturales y a la cual se le atribuye la práctica de ritos secretos. Parece ser que con el transcurso del tiempo, sus estudios derivaron también hacia la política, lo cual, hizo que finalmente se desbandaran. La contribución de los pitagóricos a la geometría fue, entre otras, el teorema que demuestra que la suma de los ángulos interiores de un triángulo es igual a dos ángulos rectos, al cual se llegó a través de los conocimientos que obtuvieron de las paralelas; propiedad de las figuras semejantes, así como una serie de estudios sobre áreas y volúmenes. Los pitagóricos proporcionaron a la geometría, sobre todo, un gran avance en el aspecto del desarrollo deductivo de la matemática. Muchos de los conocimientos geométricos los plantearon como una cadena de proposiciones sucesivas basadas en unas cuantas suposiciones iniciales y unos cuantos axiomas.
Platón (427-347 a. c.), filósofo, fue otro de los personajes que influyeron en el desarrollo de la matemática en Grecia, no por sus descubrimientos matemáticos, sino porque en su escuela era de primordial importancia que sus alumnos estudiaran geometría, ya que estaba convencido que la geometría era un campo de entrenamiento muy importante para la mente, debido a sus elementos gicos y a la más pura actitud mental que crea su estudio. A la entrada de la academia colocó un letrero que decía: «que nadie entre si no sabe geometría». Durante el siglo IV a. c., el rey Felipe de Macedonia emprendió la conquista de Persia, enemigos de los griegos. Felipe fue muerto y sucedido por Alejandro El Magno. A la muerte de Alejandro El Magno, Egipto quedó bajo el mando de Ptolomeo I, un antiguo general de Alejandro. En ese tiempo, el año 331 a. c., la capital de Egipto se estableció en Alejandría y Ptolomeo la concibió como el centro de la gran cultura griega. Fundó en 300 a. c. la Universidad de Alejandría a la cual atrajo, pagando muy buenos salarios, a los más notables artistas, filósofos, historiadores, poetas, astrónomos, etc., de la época que se desenvolvían en un, ambiente físico óptimo: atractivo edificio con grandes jardines, laboratorio, salas de lectura, así como una gran biblioteca con una colección de más de 600,000 obras. El matemático más notable en esa universidad fue Euclides, quién fundó precisamente la escuela de matemáticas de Alejandría. No se sabe cual es su fecha de nacimiento y se cree que se educó en la Escuela Pitagórica de Atenas. Euclides escribió sobre astronomía, música, óptica y otras materias, sin embargo, la obra que le dió fama universal fueron "Los Elementos", trabajo cuya mayor parte es una colección de los trabajos de sus predecesores, resumido en 13 libros o capítulos que incluyen 465 proposiciones, muchas de las cuales no son de geometría sino de teoría de números y de álgebra, escrita como una sola cadena deductiva y que por cientos de generaciones se ha conservado como un ejemplo de lógica. El Libro I contiene los conceptos iniciales, así como los teoremas de congruencia, líneas paralelas y figuras, rectilíneas. El Libro II es dedicado al álgebra, el Libro III, al círculo y el IV a la construcción de polígonos regulares. El Libro V y VI contiene la teoría de las proporciones y sus aplicaciones a la geometría. Los Libros VII, VIII y IX contienen teoría de números. El Libro X es dedicado a la teoría de los irracionales y los últimos tres a la geometrías liba, Ningún tratado ha causado un impacto tan grande sobre las matemáticas como Los Elementos, es la obra científica que más se ha editado, analizado, traducido y estudiado en el mundo. Uno de sus máximos méritos es la selección y disposición sistemática de los teoremas en un orden meticulosamente lógico, procediendo paso a paso, teorema por teorema, desde las proposiciones más simples, hasta las más complejas, estableciéndose como un modelo de razonamiento, llamado razonamiento deductivo. Es lógico pensar que no todos los trabajos eran ajenos, Euclides tuvo que hacer un buen número de demostraciones y perfeccionar otras para dar a la obra una secuencia tal, que se viera como un todo. Es lógico pensar que no todos los trabajos eran ajenos, Euclides tuvo que hacer un buen número de demostraciones y perfeccionar otras para dar a la obra una secuencia, que se viera como un todo. Después de Euclides, el matemático de más renombre fue Arquímedes de Siracusa (287 - 212 a. c.). Después de estudiar en Alejandría, regresó a Sicilia lugar donde escribió tres obras sobre geometría plana: «Medidas de una circunferencia», «Cuadratura de la parábola» y «Sobre espirales», que son ejemplos de rigor en las demostraciones. También dejó escritos sobre la esfera, el cilindro, conos, así como estudios sobre mecánica y aritmética. El tercer matemático de la antigüedad fue Apolonio, quién nació en el año 262 a. c., en Perga, al sur de Asia Menor; 25 más joven que Arquímedes, estudió en Alejandría, donde murió alrededor del año 200 a. c., Apolonio adquirió reputación entre sus contemporáneos como «el más grande geómetra» debido a su magnífica obra «Secciones cónicas», el último de los trabajos de la matemática griega considerada como una obra maestra. Escrita en ocho libros, contiene el estudio más acabado sobre el tema. La época de oro de la matemática griega llega a su fin con la muerte de Apolonio. Pocas contribuciones geométricas se hicieron después de estos grandes matemáticos. Herán (125 d. c.) calculó el área del triángulo en función de sus lados.
Menelao (98 d. c.) y Claudio Ptolomeo (168 d. c.) pusieron las bases de la trigonometría. Ptolomeo aplicó la trigonometría a la astronomía, su obra máxima es «Almagesto», una obra que es a la astronomía lo que Los elementos es a la geometría. Pappus (s IV) calcula las superficies generadas por una línea que gira alrededor de un eje situado en un plano y de volúmenes que se generan cuando se hace girar una superficie alrededor de un plano. La gran civilización griega que se había desarrollado en, Mesopotamia, en Egipto y en Grecia, fue paulatinamente destruida al ser conquistada por lo\ romanos, primeramente Grecia en el año 146 a. c. y finalmente Egipto en el año 30 a. c. El último aliento de la civilización griega se extinguió con la conquista de Egipto por los Árabes, comandados por Omar en el año 640 d. c. iniciando así la caída del imperio romano y el inicio de una época conocida como la edad del oscurantismo de Europa, por su decadencia de productividad científica y cultural, que duró hasta el siglo XII d. c. Desde el año 200 hasta el año 1200 d. c. los hindúes, influenciados de alguna manera por los griegos, habían hecho varias contribuciones a la aritmética y al álgebra. Los árabes, que a estas alturas habían extendido sus dominios sobre todas las tierras que bordean el Mediterráneo y sobre el Cercano Este agrupaban muchas razas unidas por la religión mahometana, absorbieron los conocimientos griegos e hindúes. Fue muy importante para la conservación de la cultura del mundo que los árabes asimilaran y resguardaran sus conocimientos. Numerosos trabajos hindúes y griegos referentes a astronomía, medicina y matemática, fueron diligentemente traducidos a la lengua árabe y así se salvaron hasta que posteriormente los escolares Europeos pudieron traducirlos al latín y a otros idiomas. En el año 1482 se imprimió la primera versión de la obra de Euclides. En el año 1533 se tradujo el Libro I de Comentarios sobre Euclides, de Proclo. En 1572, se tradujo Los elementos de Euclides del griego, que sirvió como base para muchas otras traducciones siguientes. Después del período del renacimiento, inició el período que corre hasta nuestros días y que se conoce con el nombre, de era moderna. Durante esta época y debido a efervescencia que causaron tantas obras de los grandes geómetras griegos, los matemáticos de la era moderna descubrieron una gran cantidad de proposiciones, a partir de las señaladas en Los elementos, dando lugar este cúmulo de conocimientos a lo que hoy se conoce como Geometría Moderna.
Geometría
La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras en el plano o en el espacio.
En el ámbito de las matemáticas, se distinguen varias clases de geometría:
Geometría algorítmica:
Aplicación del álgebra a la geometría para resolver por medio del cálculo ciertos problemas de la extensión.
Geometría analítica:
Estudio de figuras que utiliza un sistema de coordenadas y los métodos del análisis matemático.
Geometría del espacio:
Parte de la geometría que considera las figuras cuyos puntos no están todos en un mismo plano.
Geometría descriptiva:
Parte de las matemáticas que tiene por objeto resolver los problemas de la geometría del espacio por medio de operaciones efectuadas en un plano y representar en él las figuras de los sólidos.
Geometría plana:
Parte de la geometría que considera las figuras cuyos puntos están todos en un plano.
Geometría proyectiva:
Rama de la geometría que trata de las proyecciones de las figuras sobre un plano.
Euclides
Relaciones de posición que se enuncian por proposiciones tales como " La recta D es paralela a la recta D’", " la recta D es tangente al círculo C", etc.
Relaciones métricas, tales como "el segmento AB es triple del segmento AC", "la relación entre la longitud de la circunferencia y su diámetro es un número que ninguna fracción puede definir", etc.
Para establecer estas relaciones tan numerosas y variadas, los geómetras de la antigüedad pusieron a punto un método que se convertiría más adelante en el método matemático por excelencia: la demostración.
Todo el arte de los geómetras griegos consistió en reunir un conjunto importante de teoremas enlazados mediante largas cadenas de razones - como dijo Descartes- a algunos principios primeros. Este "corpus" es la geometría euclidiana.
Precisamente, el valor estético de la construcción euclídea y la trascendencia intelectual de su programa consiste en haberse propuesto eslabonar el conjunto de axiomas, definiciones y razonamientos con arte y perfección. En vez del confuso montón de intuiciones y demostraciones de los geómetras anteriores, Euclides seleccionaba unos pocos conceptos fundamentales y unas pocas relaciones entre estos conceptos, enunciadas explícitamente, para, desde aquí, pasar a la creación de nuevos conceptos y al descubrimiento de nuevas relaciones entre ellos.
La geometría de Euclides, la geometría de Descartes, la geometría de Riemann o la de Lovachevski, etc., son unas teorías deductivas. Los entes de los cuales tratan se llaman figuras y podemos dar de ellas diversas imágenes que nos permiten comunicar con nuestros semejantes. Estas imágenes pueden ser símbolos figurativos, ecuaciones, etc.
La Geometría no euclídea: Geometría para la que no es válido el axioma de paralelismo de Euclides (quinto postulados de Euclides).
La Geometría hiperbólica: Geometría no euclídea en la cual el postulado de las paralelas se sustituye por otro según el cual desde un punto exterior a una recta se pueden trazar al menos dos paralelas a ella, las cuales separan a todas las rectas que pasan por el punto en dos clases. Una, la de las que cortan a la recta dada y otra, la de las que no tienen puntos comunes con esa recta.
La Geometría elíptica: Geometría no euclídea en la cual el quinto se sustituye por otro el cual desde un punto exterior a una recta no se puede trazar ninguna recta paralela a ella.
La Geometría proyectiva: Geometría cuyos objetos son los espacios proyectivos y sus aplicaciones propias, las proyectividades.
Reseña histórica.
Es importante, antes de emprender un estudio de la geometría Euclidiana, revisar algunos antecedentes históricos que nos permita tener una visión general de su desarrollo. Tanto Proclos, como Herodoto, consignan en sus escritos que la geometría tuvo sus orígenes en Egipto con la medición de áreas, ya que el río Nílo, al desbordarse, borraba las señales que limitaban los terrenos de los agricultores. Según reseña el historiador Herodoto, en tiempos de Ramses II (1300 A. C.) la tierra del valle del Nilo se distribuía en terrenos rectangulares iguales por los cuales se debía pagar un impuesto anual, pero cuando el río invadía los terrenos, el agricultor tenía que avisar al rey lo sucedido, enviando éste a su vez a un supervisor que medía la parte en que se había reducido el terreno para que pagara sobre lo que quedaba, en proporción a impuesto que se había fijado. Precisamente, la palabra Geometría significa «medición de tierra». Afirma Herodíto que habiéndose originado la geometría en Egipto, país después a Grecia. Hay evidencias históricas, también, de aplicaciones, geométricas, algunos miles de años antes de nuestra era en regiones tales como Mesopotamia, (comprendida entre los ríos Tígris y Eufrates) y algunas regiones del centro, sur y este de Asia, en las cuales se desarrollaron grandes obras de ingeniería en la construcción de edificios y sistemas de canalización y drenaje. Los babilonios (Mesopotamia), habían desarrollado la aritmética a muy buen nivel, permitiéndoles hacer cálculos astronómicos y mercantiles. Conocían reglas (2000 - 1600 A. C.) para calcular el área de triángulos, rectángulos, trapezoides, volumen de paralelepípedos rectangulares, volumen de prisma recto, volumen de cilindro circular recto, del área del círculo (con aproximación 71= 3). Hay vestigios de que en esa época era también conocido el teorema de Pitágoras. La geometría babilónica y egipcia, como podemos apreciar era eminentemente práctica. Se le utilizaba para resolver una serie de problemas de la vida cotidiana y no como una disciplina especial, metódica. A La matemática prehelénica se, le veía como una colección de reglas para hacer cálculos que les permitía obtener resultados satisfactorios para las necesidades de la época. Alcanzaron un gran desarrollo de, la habilidad operatoria, pero sin que se presentara un sólo caso de razonamiento deductivo, como se presentó posteriormente en la etapa griega. Las relaciones matemáticas de los babilonios y egipcios fueron esencialmente formuladas, mediante el método de experimentación y error, de manera empírica, de ahí que muchas de ellas eran definitivamente erróneas.
Cualquiera que sea la conexión entre las matemáticas griegas y las de oriente, los griegos trasformaron la geometría en algo muy diferente del conjunto de conclusiones empíricas que usaron sus predecesores. Los griegos, propusieron que los hechos matemáticos deben ser establecidos por razonamientos deductivos. Las conclusiones matemáticas deben ser confirmadas mediante una demostración lógica, no por experimentación. No se sabe con certeza por qué los griegos decidieron alrededor de 600 A. C. abandonar el método empírico de obtener conocimientos matemáticos y adoptar el de razonamiento deductivo. Tal vez una de las causas sea su estructura social, pues los filósofos, artistas y matemáticos pertenecían a una clase social privilegiada que desdeñaban los trabajos manuales y las ocupaciones prácticas que eran desempeñadas por las clase más bajas, lo cual permitía a las clases privilegiadas dedicar tiempo a pensar, pues por aquel tiempo los griegos eran muy dados a hacer grandes teorías para explicar el mundo. De hecho no existen fuentes para el estudio de la geometría griega antigua, la única fuente de que se dispone, de tal época, es la obra de Proclo, conocida con el nombre de sumario de Eudemo, escrita en el siglo V D. C., y en la cual se esboza de manera muy breve el desarrollo de la geometría, desde la antigüedad hasta Euclides. El sumario de Eudemo debe su nombre a que está basado en una serie de trabajos escritos por Eudemo, discípulo de Aristóteles. Según lo relaciona el sumario de Eudemo, la geometría demostrativa se inicia en 600 a. c. con Tales de Mileto, comerciante originario de Mileto, en la costa de Asia Menor. Conocido como uno de los «siete hombres sabios» de la antigüedad, también se dedico a la filosofía, matemática, astronomía y política, frecuentemente se le llama «el padre de la geometría demostrativa», pues aplicó a sus trabajos los procedimientos del razonamiento deductivo. A Tales se le acreditan los siguientes resultados, geométricos:
Un diámetro biseca un círculo.
Los ángulos a la base de un triángulo isósceles son iguales.
Los ángulos opuestos formados por dos rectas que se intersecan son iguales.
Dos triángulos son congruentes si tienen un lado y dos ángulos iguales.
El ángulo inscrito en un semicírculo es ángulo recto (los babilonios conocían esto 1400 a los antes).
El siguiente matemático griego famoso en el sumario de Eudemo es Pitágoras, nacido aproximadamente en el año 572 a. c. en la isla de Samos, isla del mar Egeo, cercano a la ciudad de Mileto. Pitágoras, 50 años más joven que tales, razón por la cual se cree que fue discípulo de éste, es famoso no solo por el teorema que lleva su nombre, sino por sus estudios de música y sobre todo por haber fundado en el puerto de Crotona, al sur de Italia, la famosa escuela Pitagórica para el estudio de la filosofía, la música, la matemática y las ciencias naturales y a la cual se le atribuye la práctica de ritos secretos. Parece ser que con el transcurso del tiempo, sus estudios derivaron también hacia la política, lo cual, hizo que finalmente se desbandaran. La contribución de los pitagóricos a la geometría fue, entre otras, el teorema que demuestra que la suma de los ángulos interiores de un triángulo es igual a dos ángulos rectos, al cual se llegó a través de los conocimientos que obtuvieron de las paralelas; propiedad de las figuras semejantes, así como una serie de estudios sobre áreas y volúmenes. Los pitagóricos proporcionaron a la geometría, sobre todo, un gran avance en el aspecto del desarrollo deductivo de la matemática. Muchos de los conocimientos geométricos los plantearon como una cadena de proposiciones sucesivas basadas en unas cuantas suposiciones iniciales y unos cuantos axiomas.
Platón (427-347 a. c.), filósofo, fue otro de los personajes que influyeron en el desarrollo de la matemática en Grecia, no por sus descubrimientos matemáticos, sino porque en su escuela era de primordial importancia que sus alumnos estudiaran geometría, ya que estaba convencido que la geometría era un campo de entrenamiento muy importante para la mente, debido a sus elementos gicos y a la más pura actitud mental que crea su estudio. A la entrada de la academia colocó un letrero que decía: «que nadie entre si no sabe geometría». Durante el siglo IV a. c., el rey Felipe de Macedonia emprendió la conquista de Persia, enemigos de los griegos. Felipe fue muerto y sucedido por Alejandro El Magno. A la muerte de Alejandro El Magno, Egipto quedó bajo el mando de Ptolomeo I, un antiguo general de Alejandro. En ese tiempo, el año 331 a. c., la capital de Egipto se estableció en Alejandría y Ptolomeo la concibió como el centro de la gran cultura griega. Fundó en 300 a. c. la Universidad de Alejandría a la cual atrajo, pagando muy buenos salarios, a los más notables artistas, filósofos, historiadores, poetas, astrónomos, etc., de la época que se desenvolvían en un, ambiente físico óptimo: atractivo edificio con grandes jardines, laboratorio, salas de lectura, así como una gran biblioteca con una colección de más de 600,000 obras. El matemático más notable en esa universidad fue Euclides, quién fundó precisamente la escuela de matemáticas de Alejandría. No se sabe cual es su fecha de nacimiento y se cree que se educó en la Escuela Pitagórica de Atenas. Euclides escribió sobre astronomía, música, óptica y otras materias, sin embargo, la obra que le dió fama universal fueron "Los Elementos", trabajo cuya mayor parte es una colección de los trabajos de sus predecesores, resumido en 13 libros o capítulos que incluyen 465 proposiciones, muchas de las cuales no son de geometría sino de teoría de números y de álgebra, escrita como una sola cadena deductiva y que por cientos de generaciones se ha conservado como un ejemplo de lógica. El Libro I contiene los conceptos iniciales, así como los teoremas de congruencia, líneas paralelas y figuras, rectilíneas. El Libro II es dedicado al álgebra, el Libro III, al círculo y el IV a la construcción de polígonos regulares. El Libro V y VI contiene la teoría de las proporciones y sus aplicaciones a la geometría. Los Libros VII, VIII y IX contienen teoría de números. El Libro X es dedicado a la teoría de los irracionales y los últimos tres a la geometrías liba, Ningún tratado ha causado un impacto tan grande sobre las matemáticas como Los Elementos, es la obra científica que más se ha editado, analizado, traducido y estudiado en el mundo. Uno de sus máximos méritos es la selección y disposición sistemática de los teoremas en un orden meticulosamente lógico, procediendo paso a paso, teorema por teorema, desde las proposiciones más simples, hasta las más complejas, estableciéndose como un modelo de razonamiento, llamado razonamiento deductivo. Es lógico pensar que no todos los trabajos eran ajenos, Euclides tuvo que hacer un buen número de demostraciones y perfeccionar otras para dar a la obra una secuencia tal, que se viera como un todo. Es lógico pensar que no todos los trabajos eran ajenos, Euclides tuvo que hacer un buen número de demostraciones y perfeccionar otras para dar a la obra una secuencia, que se viera como un todo. Después de Euclides, el matemático de más renombre fue Arquímedes de Siracusa (287 - 212 a. c.). Después de estudiar en Alejandría, regresó a Sicilia lugar donde escribió tres obras sobre geometría plana: «Medidas de una circunferencia», «Cuadratura de la parábola» y «Sobre espirales», que son ejemplos de rigor en las demostraciones. También dejó escritos sobre la esfera, el cilindro, conos, así como estudios sobre mecánica y aritmética. El tercer matemático de la antigüedad fue Apolonio, quién nació en el año 262 a. c., en Perga, al sur de Asia Menor; 25 más joven que Arquímedes, estudió en Alejandría, donde murió alrededor del año 200 a. c., Apolonio adquirió reputación entre sus contemporáneos como «el más grande geómetra» debido a su magnífica obra «Secciones cónicas», el último de los trabajos de la matemática griega considerada como una obra maestra. Escrita en ocho libros, contiene el estudio más acabado sobre el tema. La época de oro de la matemática griega llega a su fin con la muerte de Apolonio. Pocas contribuciones geométricas se hicieron después de estos grandes matemáticos. Herán (125 d. c.) calculó el área del triángulo en función de sus lados.
Menelao (98 d. c.) y Claudio Ptolomeo (168 d. c.) pusieron las bases de la trigonometría. Ptolomeo aplicó la trigonometría a la astronomía, su obra máxima es «Almagesto», una obra que es a la astronomía lo que Los elementos es a la geometría. Pappus (s IV) calcula las superficies generadas por una línea que gira alrededor de un eje situado en un plano y de volúmenes que se generan cuando se hace girar una superficie alrededor de un plano. La gran civilización griega que se había desarrollado en, Mesopotamia, en Egipto y en Grecia, fue paulatinamente destruida al ser conquistada por lo\ romanos, primeramente Grecia en el año 146 a. c. y finalmente Egipto en el año 30 a. c. El último aliento de la civilización griega se extinguió con la conquista de Egipto por los Árabes, comandados por Omar en el año 640 d. c. iniciando así la caída del imperio romano y el inicio de una época conocida como la edad del oscurantismo de Europa, por su decadencia de productividad científica y cultural, que duró hasta el siglo XII d. c. Desde el año 200 hasta el año 1200 d. c. los hindúes, influenciados de alguna manera por los griegos, habían hecho varias contribuciones a la aritmética y al álgebra. Los árabes, que a estas alturas habían extendido sus dominios sobre todas las tierras que bordean el Mediterráneo y sobre el Cercano Este agrupaban muchas razas unidas por la religión mahometana, absorbieron los conocimientos griegos e hindúes. Fue muy importante para la conservación de la cultura del mundo que los árabes asimilaran y resguardaran sus conocimientos. Numerosos trabajos hindúes y griegos referentes a astronomía, medicina y matemática, fueron diligentemente traducidos a la lengua árabe y así se salvaron hasta que posteriormente los escolares Europeos pudieron traducirlos al latín y a otros idiomas. En el año 1482 se imprimió la primera versión de la obra de Euclides. En el año 1533 se tradujo el Libro I de Comentarios sobre Euclides, de Proclo. En 1572, se tradujo Los elementos de Euclides del griego, que sirvió como base para muchas otras traducciones siguientes. Después del período del renacimiento, inició el período que corre hasta nuestros días y que se conoce con el nombre, de era moderna. Durante esta época y debido a efervescencia que causaron tantas obras de los grandes geómetras griegos, los matemáticos de la era moderna descubrieron una gran cantidad de proposiciones, a partir de las señaladas en Los elementos, dando lugar este cúmulo de conocimientos a lo que hoy se conoce como Geometría Moderna.
Geometría
La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras en el plano o en el espacio.
En el ámbito de las matemáticas, se distinguen varias clases de geometría:
Geometría algorítmica:
Aplicación del álgebra a la geometría para resolver por medio del cálculo ciertos problemas de la extensión.
Geometría analítica:
Estudio de figuras que utiliza un sistema de coordenadas y los métodos del análisis matemático.
Geometría del espacio:
Parte de la geometría que considera las figuras cuyos puntos no están todos en un mismo plano.
Geometría descriptiva:
Parte de las matemáticas que tiene por objeto resolver los problemas de la geometría del espacio por medio de operaciones efectuadas en un plano y representar en él las figuras de los sólidos.
Geometría plana:
Parte de la geometría que considera las figuras cuyos puntos están todos en un plano.
Geometría proyectiva:
Rama de la geometría que trata de las proyecciones de las figuras sobre un plano.
Euclides
GEOMETRÍA PLANA
Un carpintero utiliza un cepillo para “aplanar” una tabla. El departamento del Petén es un departamento plano en su mayor parte. La palabra PLANO tiene un nuevo significado para usted ahora que comienza a estudiar Geometría.
Cada cosa en la vida tiene ciertas palabras que se relacionan entre si para darle significado.
En Geometría hay ciertas palabras que debemos aprender con el fin de comprender esta fascinante materia.
La Geometría es utilizada todos los día en nuestra vida, usted no podría dormir en una cama redonda, duerme en una cama rectangular.
Usted tiene un escritorio donde labora , rectangular también.
Incluso las herramientas de la agricultura como el azadón o la piocha han sido construidas basados en la geometría. Por ejemplo: la piocha; tiene un pico en forma de triangulo con el que Ud. puede cavar hoyos.
ANGULOS
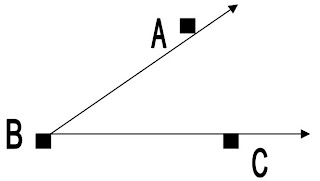Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>
Otra forma de rotular ángulos es usando la letra del vértice solamente, < B por ejemplo: pero si la figura tiene más ángulos con vértices B entonces no puede usar esta forma.
Una tercera forma de nombrar ángulos es utilizar letras minúsculas dentro de la figura como las del ejemplo siguiente.
m = medida.
< = ángulo
ABC = nombre del ángulo
39 = lo que mide el ángulo.
° = Este circulito pequeñito significa grados.
Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.
En el ejemplo anterior podemos ver que sumando las medidas de ambos 40 + 50 = 90.
Dicho en términos geométricos: m angulo ABD + m angulo DBC = 40° + 50° = 90°
A partir de ahora utilizaremos más las abreviaturas, trate de memorizar que quiere decir cada símbolo y tenga en mente que las letras señalan los puntos del ángulo.
Un carpintero utiliza un cepillo para “aplanar” una tabla. El departamento del Petén es un departamento plano en su mayor parte. La palabra PLANO tiene un nuevo significado para usted ahora que comienza a estudiar Geometría.
Cada cosa en la vida tiene ciertas palabras que se relacionan entre si para darle significado.
En Geometría hay ciertas palabras que debemos aprender con el fin de comprender esta fascinante materia.
La Geometría es utilizada todos los día en nuestra vida, usted no podría dormir en una cama redonda, duerme en una cama rectangular.
Usted tiene un escritorio donde labora , rectangular también.
Incluso las herramientas de la agricultura como el azadón o la piocha han sido construidas basados en la geometría. Por ejemplo: la piocha; tiene un pico en forma de triangulo con el que Ud. puede cavar hoyos.
DEFINICIONES
PUNTO: Un punto imaginario o escrito como el que finaliza esta frase.
Pero en Geometría el punto es la parte más pequeña que usted se puede imaginar de un punto.
PUNTO: Un punto imaginario o escrito como el que finaliza esta frase.
Pero en Geometría el punto es la parte más pequeña que usted se puede imaginar de un punto.
LINEA: Una serie de puntos conectados unos con otros de manera recta. La línea en geometría está hecha de puntos.
SEGMENTO DE LÍNEA: En cualquier línea el segmento es una parte con principio y fin.
RECTA: En una línea, una parte que consiste de un punto inicial y todos los puntos de esa línea desde ese lugar donde está el punto. Una RECTA no tiene punto final. Imagine una recta como una luz de una linterna apuntada hacia el cielo. El punto inicial es la linterna y la luz viaja hacia el infinito.
POLÍGONO: Una figura cerrada hecha de tres o más segmentos de línea.
POLÍGONO: Una figura cerrada hecha de tres o más segmentos de línea.
ANGULOS
Si dos rayas inician desde el mismo punto hacia distintos lados usted obtiene un ángulo. El punto donde comienzan las dos rayas se llama VÉRTICE DEL ANGULO. Las dos rayas se llaman lados del ángulo.
ROTULANDO ÁNGULOS
Los ángulos pueden ser rotulados o nombrados utilizando letras.
Fíjese en los tres puntos marcados en el ángulo, uno en cada lado y otro en el vértice. Cualquier ángulo puede ser rotulado marcando estos tres puntos. Es importante hacer ver que al nombrar los ángulos el vértice siempre queda entre los puntos de los lados. Este ángulo que ahora estamos estudiando puede ser nombrado como <>Otra forma de rotular ángulos es usando la letra del vértice solamente, < B por ejemplo: pero si la figura tiene más ángulos con vértices B entonces no puede usar esta forma.
Una tercera forma de nombrar ángulos es utilizar letras minúsculas dentro de la figura como las del ejemplo siguiente.
MEDICIÓN DE ÁNGULOS
Piense en cada lado de un ángulo como si fueran las manecillas de un reloj despertador, de esos de cuerda. Imagine que usted necesita darle cuerda al reloj porque se le terminó y que hay que ponerle la hora exacta. Los números o signos que hay alrededor del reloj le ayudarán a mover las manecillas tanto como lo necesite.
La unidad para medir un ángulo es el grado y el instrumento para medir ángulos es el transportador.
El transportador es una regla curva que está dividida en 180 partes iguales. La de arriba es una gráfica que ilustra como debemos utilizar el transportador para medir un ángulo.
El ángulo ABC que está siendo medido en esta gráfica mide 39°.
La unidad para medir un ángulo es el grado y el instrumento para medir ángulos es el transportador.
El transportador es una regla curva que está dividida en 180 partes iguales. La de arriba es una gráfica que ilustra como debemos utilizar el transportador para medir un ángulo.
El ángulo ABC que está siendo medido en esta gráfica mide 39°.
Como dije al principio, en Geometría debe acostumbrarse a términos y signos propios de la Geometría. No se preocupe si no se los memoriza todos rápidamente, solo trate de conservar este libro, no prestarlo, no fotocopiarlo, de esa forma le durará bastante y cada vez que necesite recordar algo podrá venir hasta aquí y consultarme.
Volvamos a la imagen ahora.
El vértice del ángulo se coloca exactamente en el medio del transportador, el lado del ángulo marcado con la letra A ha sido colocado exactamente en la posición 0° (Cero grados) y el lado marcado C nos muestra la medida del ángulo. 39°. Para abreviar medida en geometría usamos la letra minúscula m.
Toda esa palabrería que nos ha ocupado esta columna se puede abreviar simplemente así.
así. m angulo ABC = 39°. Volvamos a la imagen ahora.
El vértice del ángulo se coloca exactamente en el medio del transportador, el lado del ángulo marcado con la letra A ha sido colocado exactamente en la posición 0° (Cero grados) y el lado marcado C nos muestra la medida del ángulo. 39°. Para abreviar medida en geometría usamos la letra minúscula m.
Toda esa palabrería que nos ha ocupado esta columna se puede abreviar simplemente así.
m = medida.
< = ángulo
ABC = nombre del ángulo
39 = lo que mide el ángulo.
° = Este circulito pequeñito significa grados.
ANGULO RECTO
Es un ángulo especial cuyos lados forman una esquina cuadrada. Un ángulo recto mide exactamente 90°
En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo.
En diagramas usted puede mostrar que un ángulo es recto escribiendo 90° dentro de él. Otra forma es poner el símbolo de ángulo recto (un pequeño cuadrito en la esquina) dentro del ángulo. ANGULO LLANO
Este es un tipo especial de ángulo. Sus lados apuntan exactamente en sentidos opuestos formando una linea recta. Si usted mide un ángulo llano con un transportador encontrará que miden exactamente 180°. Esta es la medida más grande que cualquier ángulo puede tener.
TÉRMINOS GEOMÉTRICOS
GRADO: La unidad utilizada para medir ángulos.
TRANSPORTADOR: El instrumento utilizado para encontrar los grados de un ángulo.
ANGULO RECTO: Un ángulo cuya medida da exactamente 90 grados. Un ángulo recto forma una esquina cuadrada
ANGULO LLANO: Un ángulo cuya medida es exactamente 180°. Un ángulo llano forma una linea recta.
PARES ESPECIALES DE ÁNGULOS
Algunos ángulos son comúnmente encontradnos en pares. Los tres pares mas importantes son explicados de aquí en adelante.
Ángulos complementarios: Si dos ángulos juntos totalizan 90° se les llama ángulos complementarios.
Vea este ejemplo, los ángulos en este diagrama están de lado a lado pero los ángulos pueden ser complementarios sin necesidad que estén de lado a lado.En el ejemplo anterior podemos ver que sumando las medidas de ambos 40 + 50 = 90.
Dicho en términos geométricos: m angulo ABD + m angulo DBC = 40° + 50° = 90°
A partir de ahora utilizaremos más las abreviaturas, trate de memorizar que quiere decir cada símbolo y tenga en mente que las letras señalan los puntos del ángulo.
ANGULOS VERTICALES
Es otro par importante de ángulos. Son ángulos opuestos formados donde dos líneas rectas cruzan. Los ángulos verticales siempre tienen la misma medida.
Estudie este diagrama, vea que los dos ángulos angulo c y angulo d son ángulos verticales porque están de lados opuestos.
También angulo a>
ANGULOS FORMADOS POR LINEAS PARALELAS Y TRANSVERSALES
Líneas paralelas son como las líneas que un estudiante hace con su regla en un cuaderno para dibujar una línea de ferrocarril que cruza una planicie. Líneas paralelas se mantienen siempre a la misma distancia una de la otra y nunca se unen. He aquí un ejemplo:
Líneas paralelas son como las líneas que un estudiante hace con su regla en un cuaderno para dibujar una línea de ferrocarril que cruza una planicie. Líneas paralelas se mantienen siempre a la misma distancia una de la otra y nunca se unen. He aquí un ejemplo:
Por el otro lado, una línea transversal es una que cruza por sobre dos o más líneas paralelas como el siguiente ejemplo:
Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.
Ángulos especiales se forman cuando dos líneas paralelas son cruzadas por otra transversal.TÉRMINOS:
Líneas Paralelas: Líneas que van una al lado de otra, siempre a la misma distancia pero que nunca se juntan. Como las líneas del ferrocarril.
Línea Transversal: Una línea que corta o cruza dos o más líneas paralelas. Algunos matemáticos las llaman secantes.
Líneas Paralelas: Líneas que van una al lado de otra, siempre a la misma distancia pero que nunca se juntan. Como las líneas del ferrocarril.
Línea Transversal: Una línea que corta o cruza dos o más líneas paralelas. Algunos matemáticos las llaman secantes.
Ejemplo:
En los siguientes ejemplos, usted verá tres pares especiales de ángulos que se forman cuando las líneas paralelas son cruzadas o cortadas por una transversal. La primer clase se llama ángulos correspondientes. El diagrama de la siguiente página muestra que
En los siguientes ejemplos, usted verá tres pares especiales de ángulos que se forman cuando las líneas paralelas son cruzadas o cortadas por una transversal. La primer clase se llama ángulos correspondientes. El diagrama de la siguiente página muestra que
¿QUE ES GEOMETRIA?
La geometría fue, primero, la ciencia de la medida de las extensiones (geo = tierra; metrón = medida). Lo que se aprendió a medir (con los geómetras griegos) fue la extensión de una línea, recta o curva; de una superficie limitada por líneas y de un volumen limitado por superficies. Pero rápidamente la expresión medir adquirió entre los griegos un sentido muy general de "establecer relaciones". Desde las antiguas civilizaciones surgió la necesidad de medir distancias entre puntos o localidades, como así también cantidades y volúmenes de objetos, por lo que se comenzaron a conocer conceptos tales como punto, recta, plano, etc. Mas tarde seria en las civilizaciones de Egipto, Asiria, India, en donde se hablaría de figuras geométricas y la noción de ángulo, principalmente en Grecia (Siglo VI y III a.C.) donde tuvo su principal desarrollo. Durantes los años 330 y 275 a. c. en Alejandría vivió un hombre que sistematizó y amplió los conocimientos geométricos. Sin embargo en aquella época su obra, en la cual establece las relaciones entre conceptos primitivos y sus principales propiedades, pasa desapercibida. Hoy en día solo nos queda un nombre, Euclides, y a través de comentarios, la existencia de trece libros Stoikheia (elementos), en los que se encontraban los axiomas y teoremas deducidos por él, de los cuales solo nos centraremos en los cinco primeros postulados que señalan lo siguiente:
1º- Trazar una recta de un punto cualquiera a otro: (lo que equivale a decir, por dos puntos sólo pasa una recta)
2º- Prolongar por continuidad en línea recta una línea limitada: (aquí surge la confusión de suponer a la recta como línea abierta únicamente.)
3º- Describir el círculo con centro y radio dado.
4º- Todos los ángulos rectos son iguales.
5º- Si una recta al intersecar a dos rectas en un plano, forman ángulos internos sobre un mismo lado (ángulos conjugados internos) cuya suma sea menor que dos rectas; entonces las rectas, si se prolongan indefinidamente, se encontrarán del lado sobre el cual la suma sea menor que la de dos rectos.
Será finalmente este el axioma en el que nos centraremos, ya que si bien sabemos este fue motivo de discusión casi desde su misma formulación, y solo hace poco mas de un siglo se tomo la idea de tomarlo como un postulado independiente, y hace menos de cien años se demostró, efectivamente, que era imposible demostrarlo.
1º- Trazar una recta de un punto cualquiera a otro: (lo que equivale a decir, por dos puntos sólo pasa una recta)
2º- Prolongar por continuidad en línea recta una línea limitada: (aquí surge la confusión de suponer a la recta como línea abierta únicamente.)
3º- Describir el círculo con centro y radio dado.
4º- Todos los ángulos rectos son iguales.
5º- Si una recta al intersecar a dos rectas en un plano, forman ángulos internos sobre un mismo lado (ángulos conjugados internos) cuya suma sea menor que dos rectas; entonces las rectas, si se prolongan indefinidamente, se encontrarán del lado sobre el cual la suma sea menor que la de dos rectos.
Será finalmente este el axioma en el que nos centraremos, ya que si bien sabemos este fue motivo de discusión casi desde su misma formulación, y solo hace poco mas de un siglo se tomo la idea de tomarlo como un postulado independiente, y hace menos de cien años se demostró, efectivamente, que era imposible demostrarlo.
Suscribirse a:
Entradas (Atom)
